Fig. 9
Regarding the possibility of additional rotatory impact of magnets in the remaining sectors of rotation (a12 O a16, a1 O a3 and A4 O A7).
As it has been mentioned earlier, thanks to the use in the sector A8 O A11 (Fig. 2 and Fig. 5) of the levitation of permanent magnets eliminates the states of stable equilibrium, and on the motor shaft is ensured the initial rotatory torque due to the arising into the other sectors of rotation unequal lever arms of rotation around the common axis. However, as has been shown by the numerical evaluation (given in Chapter Levitation against equilibrium - the primary cause of rotation), the net torque which is produced only due to gravitational impact into the other sectors of rotation of the movable loads is relatively small, even at relatively large sizes of all parts of the device. The possibility of additional force impact in remaining sectors of rotation (in the sectors: a12 O a16, a1 O a3 and A4 O A7) initially was not obvious. So it had to make a special research, the results of which are presented in Appendix 2.... This research has revealed not only the possibility of additional contributions to the net torque by placing of the stationary permanent magnets near the other sectors of the movement of the loads, but also allowed to make recommendations for optimizing the quality of stationary magnets with respect to their geometrical shape, the direction of magnetization and screening of their lateral surfaces.
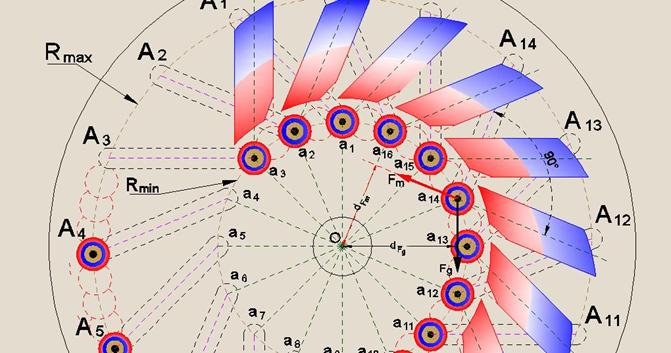
Consider Fig. 9, illustrating the mutual position of the movable and stationary magnets in sectors a12 O a16 and a1 O a3.

In this and two subsequent illustrations of this chapter are shown cross sections of the magnets by the plane which is perpendicular to the axis of rotation of the disks and passes in the middle of the space between the two disks. At this, for demonstrativeness, the cross sections of the cylindrical movable loads are shown identical, but not alternating, as it should be represented indeed at passing of the plane of cross section in such a way.
In the Fig. 9 is shown the placement of stationary permanent magnets, which is fulfilled in accordance with the above mentioned recommendations. The stationary magnets, the shape of which is close to the rectangular, are located with the minimum possible air gap with regards to the surfaces of annular magnets of the moving loads. Magnetisation of the stationary and movable magnets is such that they mutually repel each other. The centres of gravity of the cylindrical loads, during their passing through the sectors a12 O a16 and a1 O a3, are at a minimum distance (Rmin) from the axis of rotation of the disks (O).
In the sector a12 O a16 the gravitational impact on the movable loads, as well as in sector A8 O A11 (Fig. 2 and Fig. 5), hinders to rotation in the desired direction. And although this adverse effect is weaker than in the sector A8 O A11 (due to the fact that the centres of gravity of loads are at the minimum distance from the axis of rotation of the disks, during their moving into the sector a12 O a16), yet it is. This negative impact can not be eliminated by using the phenomenon of levitation, because of absence any possibility to place the stationary magnets beneath the trajectory of movement of loads into this sector. However, in this sector can ensure an additional torque in the desired direction (counter clockwise) by using the recommendations contained in Appendix 2. In the sector a1 O a3 the gravitational effect is realized in the desired direction, but it is very weak, because here the lengths of lever arms of rotation of the movable loads are too small. In this sector also can ensure an additional torque.
In Fig. 9 is shown one of the positions of rotation of the disks, in which the centre of gravity of the load a14 is located on the crossing the line of maximal counteraction of corresponding magnets with the central axis of the inclined path of this load. The angle of inclination between these two lines is 90°. The angles of inclinations of the rest stationary magnets with respect to the inclined paths of the adversarial movable loads are analogous.
This Figure shows the impact of two vectors on the center of gravity of the load a14 (the gravitational - vector Fg and the magnetic - vector Fm), i.e. impact which is transmitted through the corresponding points to the both disks. Here are also shown the lever arms of rotation which are correspond to the indicated vectors (dFg and dFm). At this, the vector Fm should be understood as the result of a complex interaction of magnetic fields emanating from the opposing surfaces of the movable magnet and the stationary magnet.
Figure 9 illustrates that in both these sectors the vectors of magnetic impact are directed counter clockwise, that is, they provide an additional torque in the desired direction. Thus, the above mentioned disposition of stationary magnets, focused on the repulsion of ring magnets of the movable loads in the sectors a12 O a16 and a1 O a3, increases the net torque on the shaft of motor.
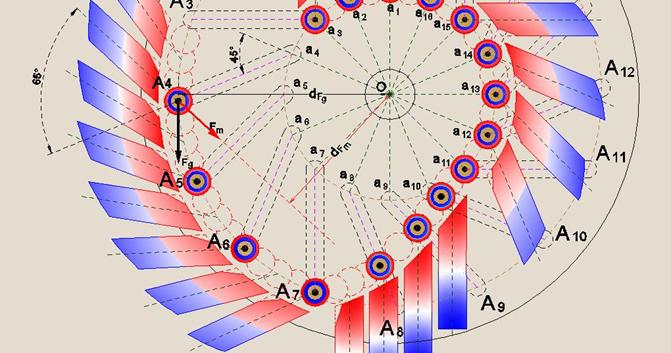
In the sector A4 O A7 (Fig. 10), where the trajectory of movement of the centres of gravity of the movable loads is removed from the axis of rotation of the disks at the maximum distance (Rmax), that is, into the sector where the positive gravitational impact on the net torque is maximally, also its possible make contribution to increase of net torque by using the analogous method.
In Fig. 10 is shown the mutual disposition of the movable and stationary magnets in the sector A4 O A7 in one of the moments of rotation of the disks, in which the centre
The dimensions of the angles of inclination of stationary magnets, which are indicated in Figures 9 and 10, seem to be optimal, although the accuracy of such recommendations must be refined in the process of experimental testing.
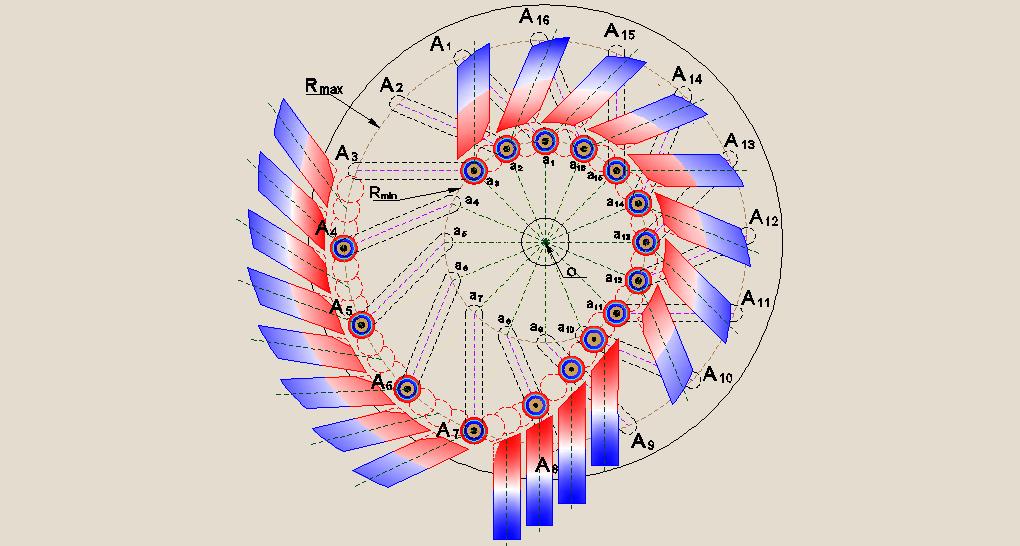
In Fig. 11 is schematically shown the complete picture of the mutual location of the stationary permanent magnets, the shape of which is close to rectangular, and of the movable cylindrical loads, equipped with annular magnets, during their moving.
Here can be seen the mutual placement of the stationary and movable magnets in the sector A8 - O - A11, where, due to the levitation of loads, are provided the conditions for creation of the initial rotatory impact through the use of the kinetic energy of gravitation in the sectors A4 O A7 and a12 O a15, into which centers of gravity of the opposed movable loads are linked with unequal lever arms about the axis of rotation of the rotor (point O), and at this, can be seen in this figure the placement of stationary magnets near the sectors A4 O A7, a12 O a16 and a1 O a3, where, due to the interaction of stationary and movable magnets, is created the additional rotatory impact through the use of magnetic energy.

The rotor of motor surrounded by the stationary magnets

View of the rotor and stator without the front disk
Figures 12 and 13 show, for clarity in three dimensions, the essence of the design of the rotor and the stator of the proposed motor.
Thus, the stated above additional placement of the stationary permanent magnets, providing a repulsive impact on the annular magnets of the cylindrical loads, during their moving in the sectors: a12 O a16, a1 O a3 and A4 O A7, is able to ensure an additional increase of the net torque on the motor shaft.
This page was last modified on 28 September 2014